Noise and Vibration Problems in Tube Bundles by V.Ganapathy

 

Introduction
Tube bundles in heat exchangers,boilers,superheaters,economizers and air heaters are often subject to vibration and noise problems. Vibration can lead to wear and consequent tube failures.Large gas pressure drop across the equipment is also a side effect.Noise problems can be a nuisance to operating personnel.This article deals with vibration problems which occur in cross-flow situations in steam generator components.
Whenever gas(or air) flows over a tube bundle in inline or staggered arrangement,vorticies are formed and shed beyond the wake of the tubes,resulting in harmonically varying forces perpendicular to the flow direction.It is a self excited vibration and the frequency of vibration is called vortex shedding frequency.If the frequency of vibration of the Von-karman vortices as they are called coincide with the natural frequency of vibration of the tubes, resonance occurs leading to bundle vibration.
Another phenomenon that occurs with vortex shedding is acoustic vibration,leading to noise and high gas pressure drop.Standing waves are formed inside the duct.The acoustic pressure fluctuations are a maximum where the fluid motion is zero;hence the walls of the enclosure are subject to pressure pulsations and may distort outwardly.The duct or the bundle enclosure vibrates when the vortex shedding frequency coincides with the acoustic frequency.Though a few simple checks are proposed below,there are by no means complete. Experience with similar sized units,tube spacings and tube size is helpful in predicting probability of vibration problems.

Design methods to check vibration and noise  
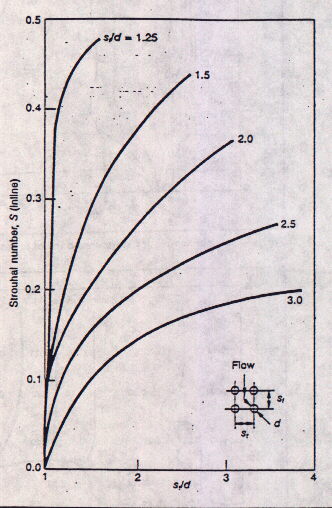
The first step in the analysis of bundle vibration and noise is the estimation of the vortex shedding frequency fe,cycles/s.This may be obtained from Strouhl number S.  
S=fe d/(12V),where d=tube OD,in and V=gas velocity,ft/s.Figure above shows typical S values for inline tube bundles per Chen. There are also similar charts developed by Fitzhugh and others; it may be noted that for the same values of tube bundle spacings, different charts give different S values,leading to different vortex shedding frequencies. Hence in the author's view the results of vibration analysis is still subject to interpretation and judgement calls and not like the computation of say gas velocity,where everyone comes up with nearly the same answer! Calculations apart,experience based on similar sized units in operation is a big help in determining if noise or vibration is a concern.The author's books show the other charts for staggered arrangements developed by Fitzhugh and Chen.  
Natural frequency of vibration of tubes,fn  
For a uniform carbon steel tube supported at ends, fn,is obtained by the formula:  
fn=90C[(d4-di4)/M]0.5/L2  
where L is the span in ft,M=mass of tube including the fluid inside,lb/ft and d,di are the outer and inner diameters,in.C is a constant. For clamped ends,C=22.37 ,61.67 and 120.9 in modes 1,2 and 3 respectively.  
Acoustic frequency ,fa.  
fa=Vs/(2w/n),where w=width of bundle,ft,n= mode of vibration and Vs=sonic velocity.ft/s.  
For air and flue gases,Vs can be shown in rectangular ducts to be about 49(460+t))0.5  
where t= gas temperature,F.  
Checks for vibration and noise  
1.Calculate fn for different modes.Compute fe at different loads. If fe and fn are within 20% then vibration is likely,particularly if it is in mode 1,which has the highest amplitude of vibration.  
2.Estimate fa at different loads.Compare fa  with fe. If within 20%, then acoustic vibration and noise is likely.  
Eliminating noise problem  
Acoustic baffles are widely used to eliminate noise concerns. When a baffle is inserted in the tube bank,reducing the width by half or a third,the acoustic frequency doubles or triples as shown in the equation above.(w is reduced when the baffle is inserted).Inserting two baffles would triple the acoustic frequency.Hence the vortex shedding and acoustic frequency are kept wide apart.  
Similarly if tube bundle vibration is seen,then intermediate tube supports may be used to change the natural frequency of the tubes or the length or tube size may be varied to minmize the concern.  
 		 Example  
A tubular air heater 11.7 ft wide,15 ft deep and 13.5 ft high(length) is used in a boiler.Carbon steel tubes of size 2x0.08 in are used in inline fashion with a transverse pitch(st) of 3.5 in and longitudinal pitch(sl) of 3 in.There are 40 tubes wide (3.5 in pitch) and 60 tubes deep(3 in pitch).300,000 lb/h of air at an average temperature of 219 F and atmospheric pressure flows across the tubes.The tubes are fixed at both ends.Tube mass per unit length=1.67 lb/ft.Check for noise and vibration problems.   
Solution  
Let us compute fa,fe and fn. L=13.5 ft,d=2,di=1.84 in,M=1.67 and C=22.37   
fn=90x22.37x[(24-1.844)/1.67]0.5/13.52 =18.2 c/s in mode 1. In mode 2,C=61.67 and fn=50.2 c/s  
Let us compute fe.S for st/d=1.75 and sl/d=1.5,S=0.33 from figure above.   
air density at 219F=40/(460_219)=0.059 lb/ft3  
Free gas area=40x93.5-2)x13.5/12=67.5 lb/ft2  
air velocity across tubes=300,000/(67.5x3600x0.059)=21 ft/s  
Hence fe=12SV/d=12x0.33x21/2=41.6 c/s  
Compute fa. Vs=49x(219+460)0.5=1277 ft/s. width w=11.7 ft. hence fa=1277/23.4=54.5 c/s in mode 1 and 109 c/s in mode 2.  
Hence it is seen that in mode 1,fa and fe are close suggesting possible noise problems. fn is far apart from fe and hence tube vibration is not a concern. If we inserted a baffle dividing the width into nearly two equal halves,then the acoustic frequency in mode 1 is 109 c/s,far apart from fe,eliminating the acoustic vibration concern.  
 
Conclusion
Vibration calculations are often subject to controversy as the vortex shedding frequencies can be different with different Strouhl numbers from various charts. Also it is often difficult to isolate the cause of vibration due to environmental factors. Experience is very helpful in dealing with these issues as calculations sometimes could suggest  problems when there is none and vice versa.Sometimes the vortex shedding frequencies coincide with transverse acoustic frequencies and yet no standing waves are formed. A damping criterion has been proposed by some engineers based on tube spacings.There are papers which point out that the damping criterion for bare tubes is 600 and about 15,000 for finned tube bundles. These are based on specifc studies and may have limitations when used in broad context.Finned tube bundles have more damping effect in general and hence compared to bare tube bundles they have fewer problems.However there could be exceptions.

 Books,Software,Papers on Boilers,HRSGS,Steam plant calculations
 email Ganapathy